KLV大学 ハイパースペクトルカメラコース
ハイパースペクトルカメラコース
スペクトルカメラ知識コンテンツ
スペクトルカメラ技術基礎
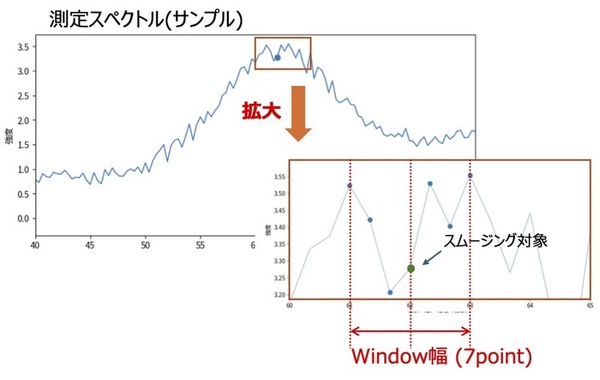
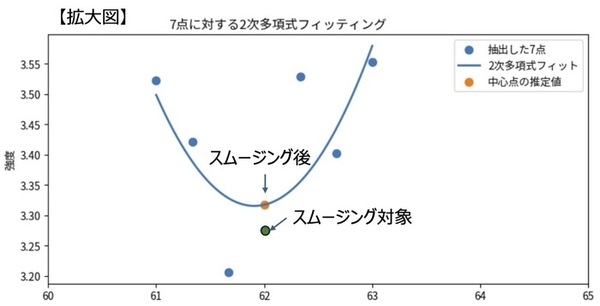
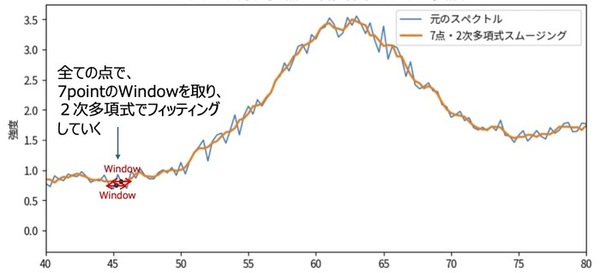
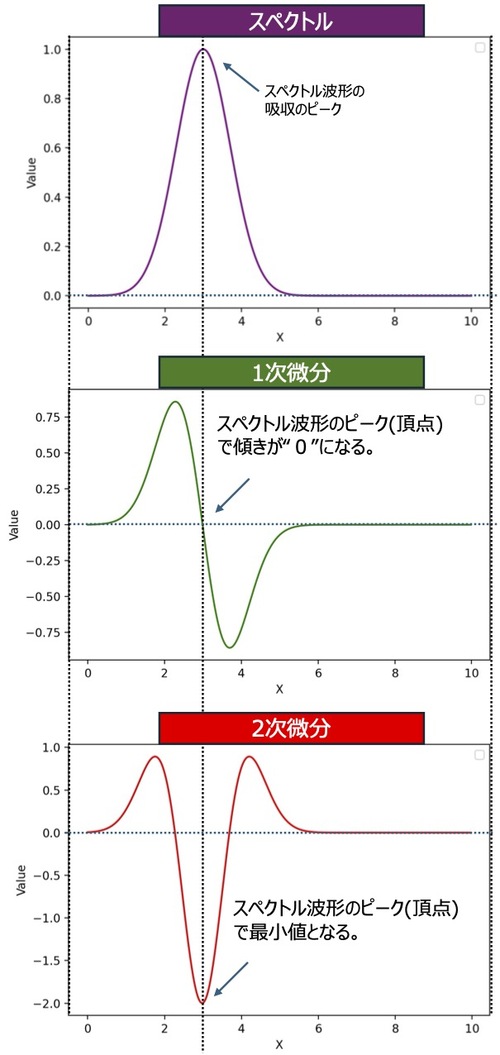
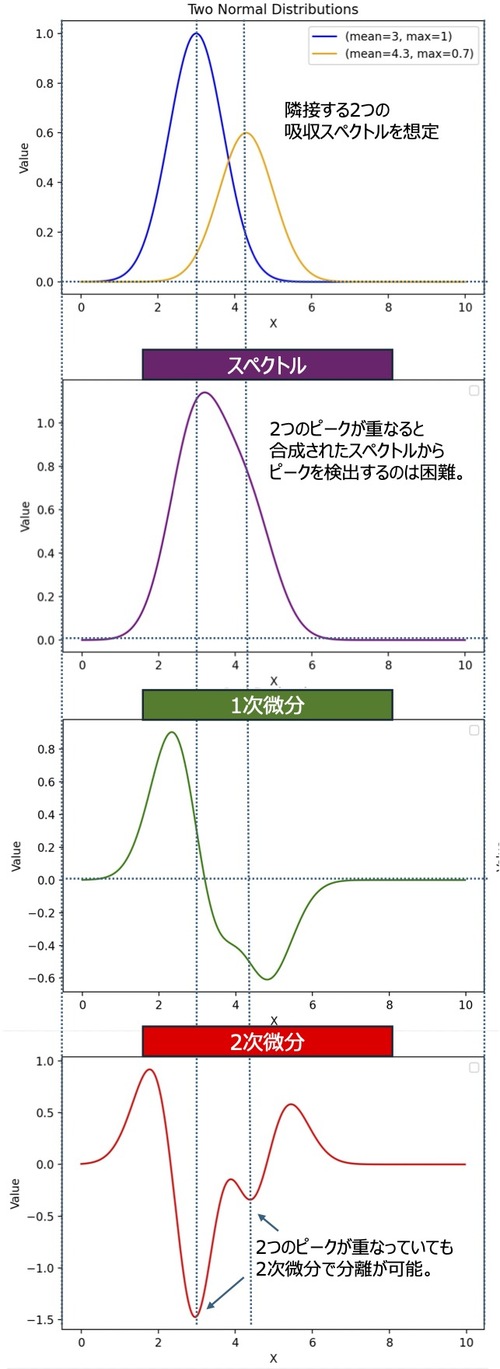
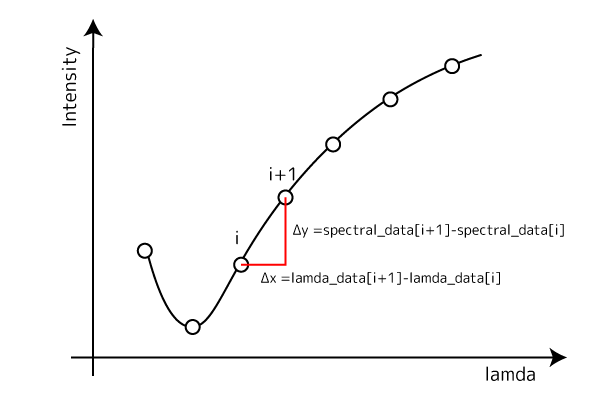
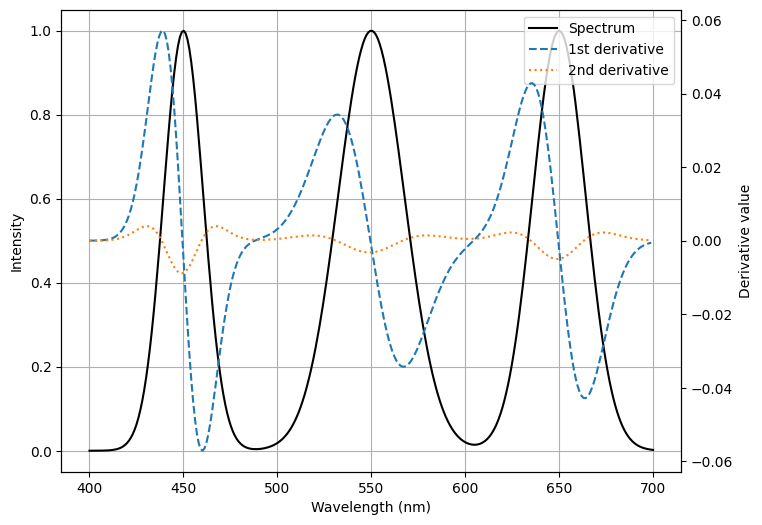
スペクトル解析
スペクトルカメラ論文
スペクトルカメラの選び方
スペクトルカメラのデモ
スペクトルカメラアプリケーション
- ハイパースペクトルカメラで樹脂や金属の劣化を読み解く新技術
- SDGsと光学機器・センサー
- ハイパースペクトルカメラ事例集
- 見えない異物を検出
- 人手不足の現状と次世代の省人化技術、ハイパースペクトルカメラの可能性
- ハイパースペクトルカメラによるカーボンニュートラル実現に向けた技術革新の効率化
- ハイパースペクトルカメラで加速する脱プラスチック
- ハイパースペクトルカメラがもたらすDX
- 膜厚測定
- クロロフィル測定とは?
- 偽造防止印刷とは?
- 近赤外分光で繊維選別
- ハイパースペクトルカメラ事例|工業分野
- プラスチック資源循環促進法とは
- 近赤外分光でプラスティック選別
- 半導体・フィルムの膜厚測定
- マシンビジョンでの活用事例
- ハイパースペクトルカメラ事例|食品分野
- 食品産業業界の未来を考える
- 食品産業で活躍するIoTセンサー
- ハイパースペクトルカメラ事例|医療分野
- 医療分野での活用
- ハイパースペクトルカメラ事例|インフラ分野
- インフラ(コンクリート)の維持保全
- ハイパースペクトルカメラ事例|防衛・セキュリティー分野
- ハイパースペクトルカメラ事例|リモートセンシング
- ハイパースペクトルカメラ事例|農業分野